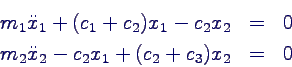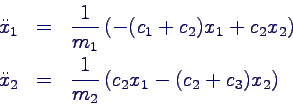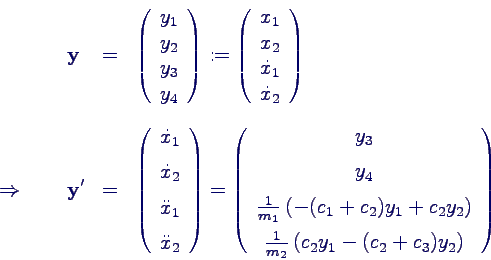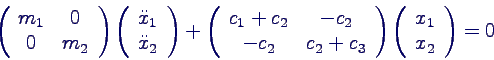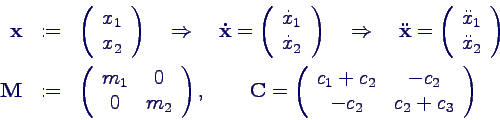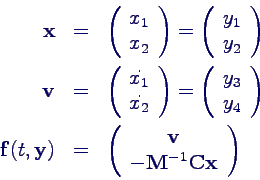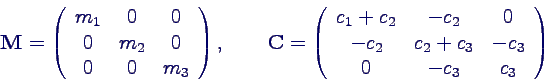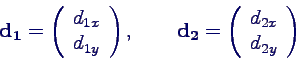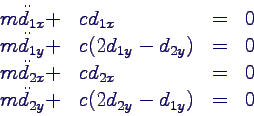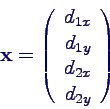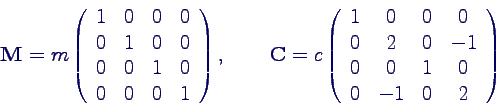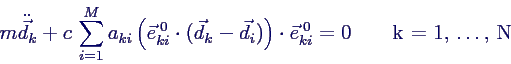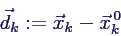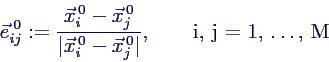Mehrdimensionale Schwingungen

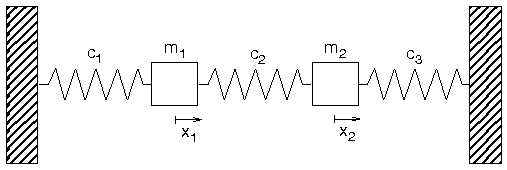
• Zweidimensionale Schwingerkette:
  • 2 Massen, mit Federn gekoppelt
    • 
  • Bewegungsgleichung
    • 
  • vgl. Applet Coupled Oscillators
    • 
  • Bewegungsgleichung nach höchsten Ableitungen auflösen
    • 
  • in Grundform bringen
    • 
  • rechte Seiten als Matlab-Funktion schwing2d.m
  • Anfangsbedingung: Massen in Ruhe, nur 1. ausgelenkt
  • Lösen
    • [t, y] = ode45(@schwing2d, [0 30], [1 0 0 0]);
  • Plot der Bewegungen
    • 1./2. Spalte = x₁/x₂
    • 3./4. Spalte = v₁/v₂
    • plot(t, y(:,1), t, y(:,2))
      legend("x_1(t)", "x_2(t)", "Location", "best");
    • 
• Matrixform der Schwingungsgleichung:
  • Bewegungsgleichung umschreiben
    • 
  • Vektoren und Matrizen einführen
    • 
  • Bewegungsgleichung lautet dann
    • 
  • M heißt Massenmatrix, C Steifigkeitsmatrix
  • für die Grundform y in Zweiervektoren zerlegen
    • 
  • rechte Seiten mit Parametern M, C, als Matlab-Funktion matschwing2d.m
  • Matrizen M, C und Hilfsfunktion definieren
    • M = [m1, 0; 0, m2];
      C = [c1+c2, -c2; -c2, c2+c3];
      fhilf = @(t,y) matschwing2d(t, y, M, C);
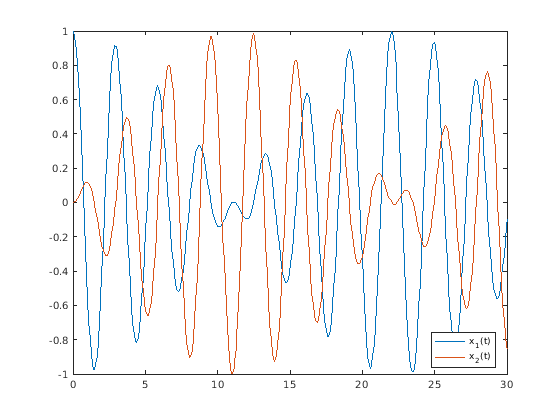
  • Anfangsbedingung: Massen in Ruhe, 1. und 2. gegeneinander ausgelenkt
  • Lösen
    • [t, y] = ode45(fhilf, [0 30], [1 -1 0 0]);
    • 
• N-dimensionale Schwingungen:
  • mehrere Massen und/oder Bewegung in mehr als einer Dimension
  • Schwingungsgleichung in Matrixform bleibt gültig
  • Beispiel "Schwingendes Hochhaus"
    • 
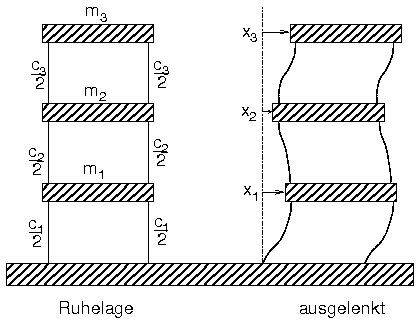
    • Matrizen
    • 
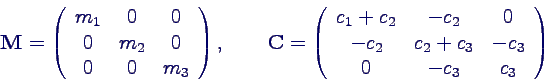
  • Matlab-Funktion schwingNd.m zerlegt Vektor y in zwei Teile
  • Lösen mit Anfangsgeschwindigkeit für v₃ mit Matlabskript bild26.m
    • 
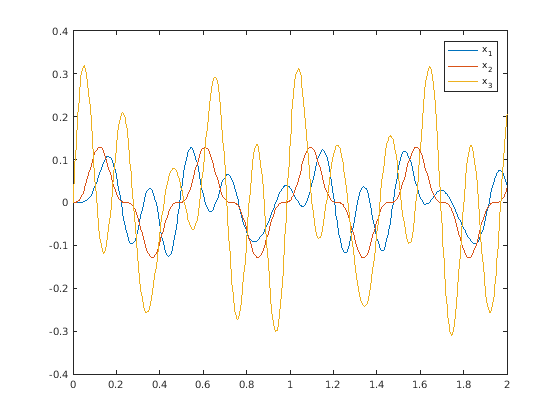
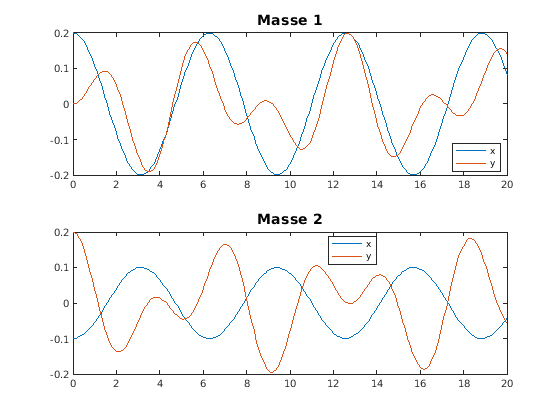
• Bewegung in zwei Dimensionen:
  • Beispiel
    • 
  • Verschiebungen d_i der Massen: 2 Vektoren mit jeweils 2 Komponenten
    • 
  • Bewegungsgleichungen
    • 
  • Reihenfolge der Koordinaten festlegen
    • 
  • dann kann man die Matrizen ablesen
    • 
  • Lösen und plotten mit Matlabskript bild28.m
    • x- und y-Koordinaten
    • 
    • Bahnkurven
    • 
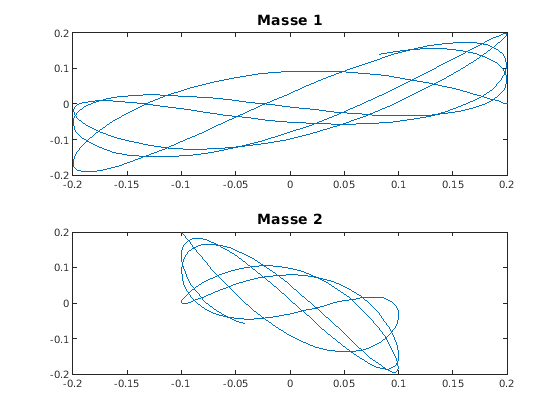
  • Bewegung schwer nachzuvollziehen, besser mit Animation
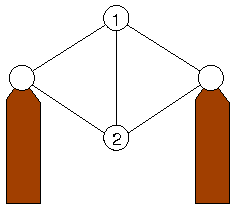
• Schwingungen eines Fachwerks:
  • Aufstellen der Bewegungsgleichungen
    • mühsam (vgl. fachwerk.pdf)
    • Ergebnis
    • 
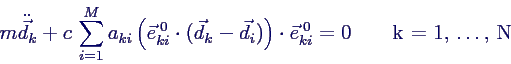
    • für die Abweichungen von der Gleichgewichtslage
    • 
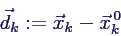
    • mit den Richtungsvektoren
    • 
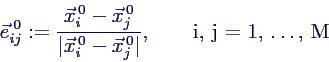
  • Ermitteln der Steifigkeitsmatrix
    • erledigt Routine createMatrices
    • Reihenfolge der Koordinaten x₁, y₁, x₂, y₂, ..
  • bequemes Lösen der DGL mit solveVibrationODE
    • Anfangsauslenkungen d0 als N 2d-Spaltenvektoren in einer Matrix
    • Anfangsgeschwindigkeiten v0 ebenso
    • Ergebnisse d, v als (NT x 2 x N)-Tensor
  • Umsortieren mit reshape(A, N, M)
    • ordnet erst alle Spalten von A untereinander zu langem Vektor
    • teilt dann neu auf in NxM-Matrix
  • Funktionen mit optionalen Parametern
    • hintere Argumente können weggelassen werden
    • Variable nargin enthält Zahl der übergebenen Parameter
    • Funktion prüft nargin und definiert ggf. Standardwerte
• Aufgaben:
  • Aufgabe 12
  • Aufgabe 13