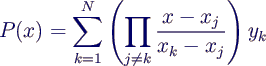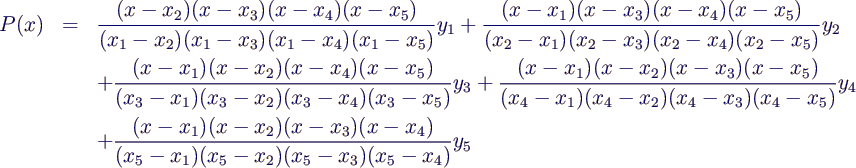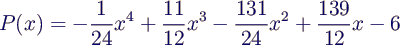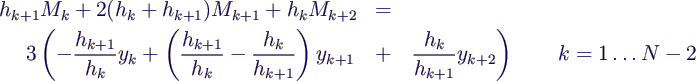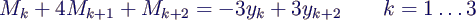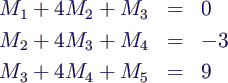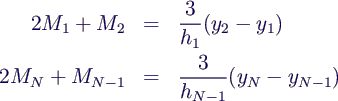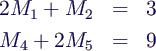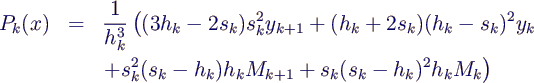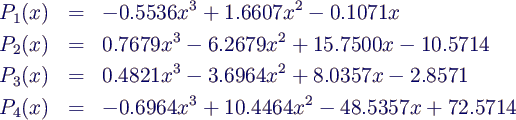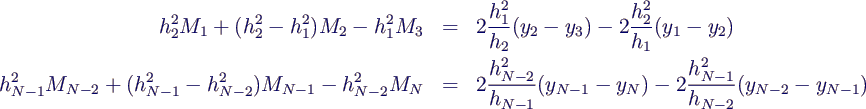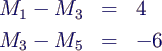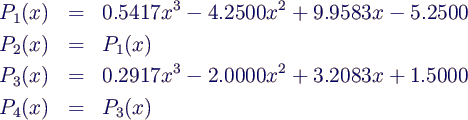Lösung von Aufgabe 9

1. Interpolationspolynom:
   • Für N = 5 liefert die allgemeine Formel
     • 
   • die konkrete Version
     • 
   • Einsetzen der Werte ergibt dann (nach endlichem Rechnen)
     • 
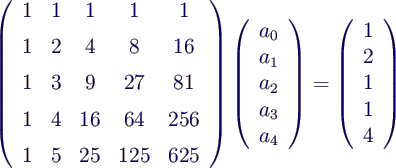
   • Wem die Rechnung zu lang ist (oder wer keinen symbolischen Rechner hat), der kann stattdessen auch das Gleichungssystem mit der Vandermonde-Matrix lösen:
     • 
   • liefert das gleiche Ergebnis (numerisch natürlich).
2. Spline-Interpolationsfunktionen:
   • Gesucht sind die Polynome P₁, P₂, P₃, P₄ auf den entsprechenden vier Intervallen.
   • Als erstes werden die Intervallbreiten h_i bestimmt, sie sind hier
     • h_i = 1, i = 1 .. 4
   • Die Formel für die Steigungen
     • 
   • vereinfacht sich dann zu
     • 
   • also konkret
     • 
   • Für natürliche Splines kommen noch die Gleichungen
     • 
   • dazu, konkret also
     • 
   • Diese 5 Gleichungen lassen sich mit Matlab schnell lösen, man erhält als Steigungen
     • M_i = [1.5536, -0.1071, -1.1250, 1.6071, 3.6964]
   • Dies in die Formel
     • 
   • eingesetzt liefert
     • 
   • Analog hat man für not-a-knot-Splines die zusätzlichen Gleichungen
     • 
   • konkret
     • 
   • Damit erhält man die Steigungen
     • M_i = [3.0833 -0.5417 -0.9167 1.2083 5.0833]
   • und die Polynome
     • 

• graphische Darstellung der Interpolationsfunktionen
  • 
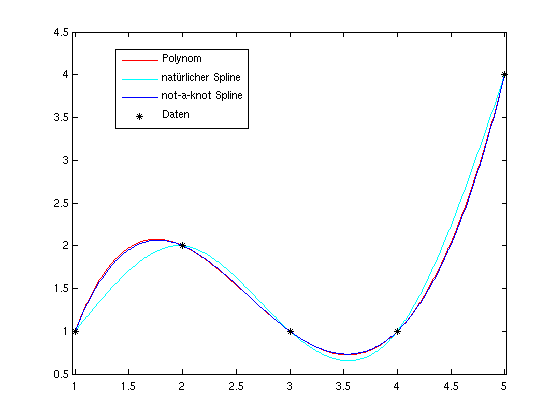
  • der natürliche Spline läuft an den Rändern geradlinig aus
  • Polynom (4. Ordnung) und not-a-knot-Spline (2x 3. Ordnung) sind kaum zu unterscheiden
  • Reproduktion aller Ergebnisse mit dem Matlab-Skript ex09.m