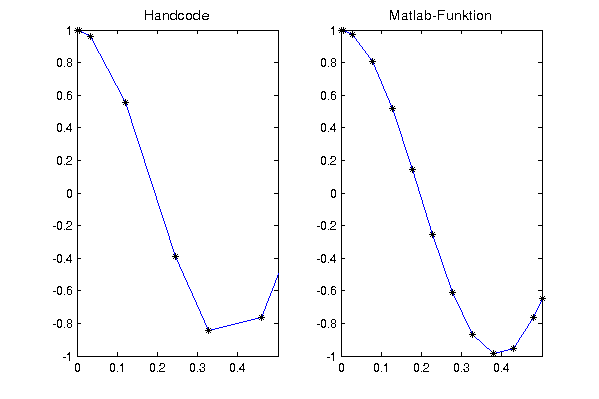
Lösung von Aufgabe 21

• Alle Berechnungen können mit dem Matlab-Skript ex21.m ausgeführt werden.
• Zunächst muss die Differentialgleichung - wie oben beschrieben - in die Grundform gebracht werden. Die Funktion f kann dann z. B. definiert werden durch
  • omega = 8.0;
    f = @(t,y) [y(2); -omega^2*y(1)];
• Die einzelnen Formeln des Algorithmus lassen sich direkt nach Matlab übertragen, wenn man noch die Beträge bei Vektoren durch die norm()-Funktion ersetzt.
• Alternativ zur Handarbeit können die einzelnen Zeitschritte bis zum Überschreiten der Endzeit bequem in einer while-Schleife durchlaufen werden. Dabei werden die anfallenden Ergebnisse (Zeiten und y-Werte) zur späteren Auswertung in Arrays tall und yall gesammelt.
• Man erhält dann folgende Schritte:

  • h	t	epslok
    0.0058	0.0058	0.000017	ok
    0.0290	0.0348	0.001933	ok
    0.0865	0.1213	0.017935	ok
    0.1227	0.2440	0.007227	ok
    0.2356	0.2440	0.323707	zu groß
    0.1274	0.2440	0.187370	zu groß
    0.0827	0.3266	0.012660	ok
    0.1317	0.4584	0.069428	ok
    0.1190	0.5774	0.010382	ok

• Vergleich mit Matlabs ode23:
  • 
• Am auffälligsten ist die generell kleinere Schrittweite bei Matlab. Ursache ist die Beschränkung von h auf maximal 1/10 des Zeitintervalls. Dadurch ist das Ergebnis insgesamt genauer als der Handcode, aber auch genauer als gefordert. Durch Vergleich mit der bekannten Lösung
  • x(t) = cos(ω t)
• erhält man leicht den tatsächlichen maximalen Fehler
  • errMax(Handcode) = 0.1005
  • errMax(Matlab) = 0.0089
• Außerdem wird bei Matlab die Endzeit genau erreicht, während der Handcode darüber hinausschießt. Dies lässt sich durch eine Anpassung der Schrittweite am Ende leicht erreichen.