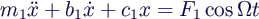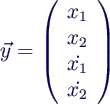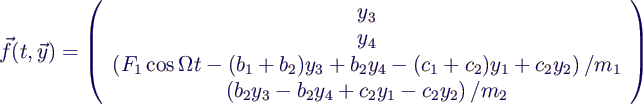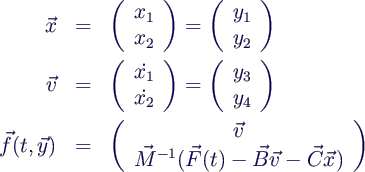Lösung von Aufgabe 20

• Alle Berechnungen können mit dem Matlab-Skript ex20.m ausgeführt werden.

• ohne Tilger:
  • Im Fall ohne Tilger vereinfacht sich die Bewegungsgleichung zu
    • 
  • Die entsprechende Systemfunktion incl. aller Parameter ist schnell hingeschrieben:
    • function dydt = f1d(t, y, m, b, c, F, Om)
      % rechte Seite der DGL bei erzwungener Schwingung ohne Tilger
      x = y(1);
      v = y(2);
      dydt = [v; (F*cos(Om*t) - b*v - c*x)/m];
  • Für den Solver muss eine Hilfsfunktion eingeführt werden, die nur von t und y abhängt:
    • f1 = @(t,y) f1d(t,y,m1,b1,c1, F1, Om);
  • Dann kann mit dem Standardsolver ode45 das Problem sofort gelöst werden:
    • [t, y] = ode45(f1, [0 60], [0 0]);
      x = y(:,1); % Auslenkung
      v = y(:,2); % Geschwindigkeit
      plot(t, x);
      xlabel("t [s]","FontSize",12);
      ylabel("x [m]","FontSize",12);
    • 
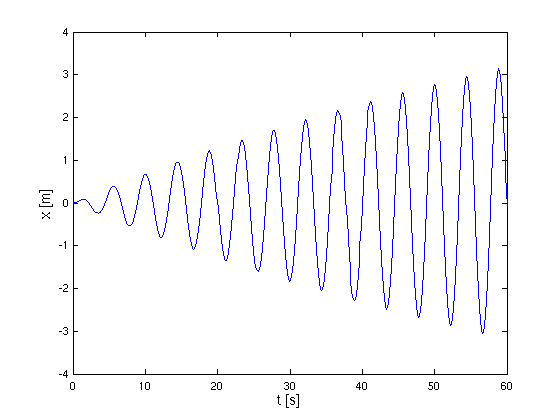
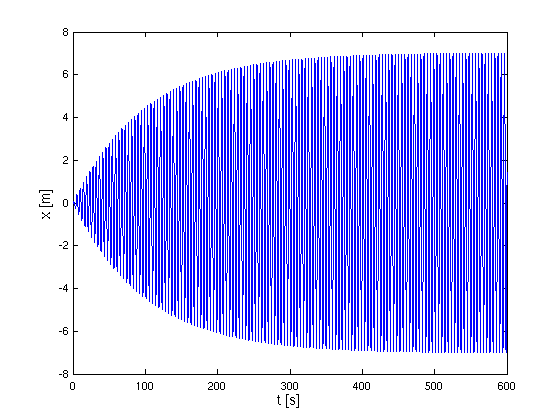
  • Der Plot zeigt, dass sich die Schwingung der Masse noch aufschaukelt, man muss für die Dauerschwingung also länger simulieren. Für t₁ = 600 s erhält man
    • 
  • Aus dem Bild kann man die erreichte Amplitude ungefähr ablesen. Genauer geht es, indem man die Daten aus der Simulation direkt verwendet. Dazu werden zunächst die Werte nach t = 500 s herausgefiltert, dann unter diesen das Maximum herausgesucht:
    • index = find(t >= 500);
      xSpaet = x(index);
      amplitude1d = max(abs(xSpaet))
  • Man erhält eine Amplitude von 7.0085 m. Bei genauerer Betrachtung stellt man übrigens fest, dass die Amplitude immer noch - wenn auch nur leicht - ansteigt!
• mit Tilger:
  • Im Fall mit Tilger hat man zwei Gleichungen jeweils zweiter Ordnung, man braucht also einen Vektor mit insgesamt 4 Zustandsgrößen. Am einfachsten definiert man
    • 
  • Schreibt man die Matrix-Vektor-Multiplikationen komponentenweise aus, kann man die Systemfunktion leicht hinschreiben:
    • 
  • Eleganter und - spätestens bei größeren Systemen - übersichtlicher wird es, wenn man y in Zweiervektoren zerlegt und die Matrizen stehen lässt:
    • 
  • In Matlab lautet die entsprechende Funktion dann einfach
    • function dydt = f2d(t, y, M, B, C, Fhat, Om)
      % rechte Seite der DGL bei erzwungener Schwingung mit Tilger
      x = y(1:2);
      v = y(3:4);
      dx = v;
      dv = inv(M)*(Fhat*cos(Om*t) - B*v - C*x);
      dydt = [dx; dv];
  • Das kann wieder leicht mit ode45 integriert werden, man erhält
    • 
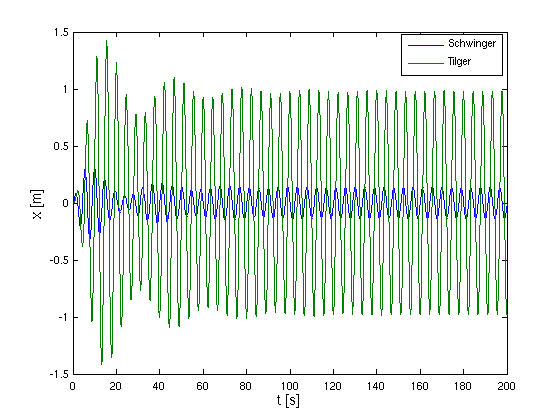
  • Spätestens ab t = 100 s ist die Dauerschwingung erreicht. Wie oben erhält man eine Amplitude von 0.1413 m für den Schwinger und von 0.9942 m für den Tilger. Das Maximum über alle Tilgerauslenkungen zeigt, dass er in der Einschwingphase bis auf 1.4287 m ausgelenkt wird.