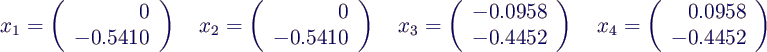Lösung von Aufgabe 16
- Alle Berechnungen und Zeichnungen können mit dem Matlab-Skript
ex16.m ausgeführt werden.
- Die Massen- und die Steifigkeitsmatrix definieren das
verallgemeinerte Eigenwertproblem, das in Matlab mit
- sofort gelöst werden kann.
- Die Eigenwerte di auf der Diagonalen von D sind
die Werte ωi2, die Eigenfrequenzen fi
erhält man dann als
- Für gewöhnlich sortiert man die Eigenwerte der Größe
nach, bei Schwingungsproblemen beginnend mit dem kleinsten. Die ersten (niederfrequenten)
Schwingungen lassen sich in der Regel leichter anregen und sind daher in der
Praxis am bedeutendsten.
- Die Eigenvektoren sind jeweils die Spalten von U, der 1. Eigenvektor
(zur Eigenfrequenz f1 = 0.0670 Hz) ist also
- Gemäß der Definition der Komponenten
von
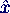 bedeutet dies folgende
Verschiebungsvektoren für die vier Knoten:
bedeutet dies folgende
Verschiebungsvektoren für die vier Knoten:
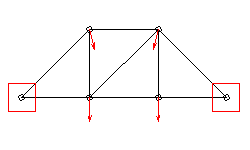
- Zeichnet man diese Vektoren direkt an die Knoten, erhält
man eine gute Vorstellung von der Form der 1. Eigenschwingung
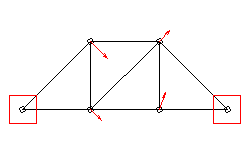
- bzw. analog von der 2. Eigenschwingung zur Frequenz f2
= 0.0984 Hz
- Statt selbst zu zeichnen, kann man das auch Matlab erledigen
lassen. Dies erledigt hier die
Routine plotMode(xe) in folgender Weise
- x0 enthält die x- und
y-Koordinaten der 6 Punkte (1 - 4 beweglich, 5 und 6 fest).
- A ist eine symmetrische
6x6-Matrix mit Einträgen 0 und 1. Dabei bedeutet aij =
1, dass die Punkte i und j durch eine Feder verbunden sind.
- Die Massen werden einfach als kleine Kreise
geplottet.
- In einer Schleife über die Elemente von A werden
die Federn als Verbindungsstrecken der Punkte gezeichnet.
- Die Vektoren werden mit der
Funktion quiver erzeugt. Diese enthält
für jeden Vektor x- und y-Koordinate des Angriffspunktes
(aus x0) und x- und y-Koordinate des Vektors
selbst (in xe).



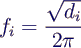
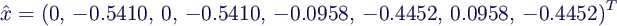
 bedeutet dies folgende
Verschiebungsvektoren für die vier Knoten:
bedeutet dies folgende
Verschiebungsvektoren für die vier Knoten: