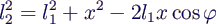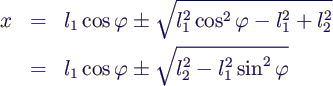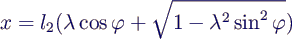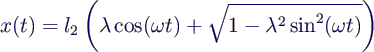Lösung von Aufgabe 14

1. Berechnung der Ortskurve:
   • Der Cosinussatz für das Dreieck OPQ liefert
     • 
   • Nach x auflösen →
     • 
   • Negatives Vorzeichen entfällt wegen l₂ > l₁, x > 0. Einführen von λ ergibt
     • 
   • Gleichmäßige Umdrehung heisst
     • φ = ω t
   • also
     • 
   • Die Parameter l₂ und ω spielen für die Form von Ortskurve und Spektrum keine entscheidende Rolle:
     • l₂ skaliert (bei festem Schubstangenverhältnis λ) lediglich x(t), ist also für alle Fourierkoeffizienten ein gemeinsamer Faktor;
     • ω tritt nur als Faktor von t auf, gibt also die Grundfrequenz vor und streckt das Spektrum, ohne seine Form zu beeinflussen.
   • Im Weiteren werden sie fest gewählt zu
     • l₂ = 1
     • ω = 2 π (also T = 1)
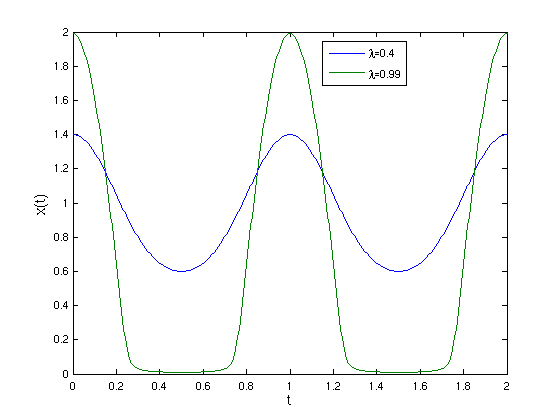
   • Plot
     • 
2. Bestimmung des Spektrums:
   • Zunächst werde mit großen Werten für T und N gerechnet, um eine möglichst genaue Darstellung zu erhalten:
     • T = 100;
     • N = 4096;
   • Die zugehörige Nyquistfrequenz ist f_N = 20.475
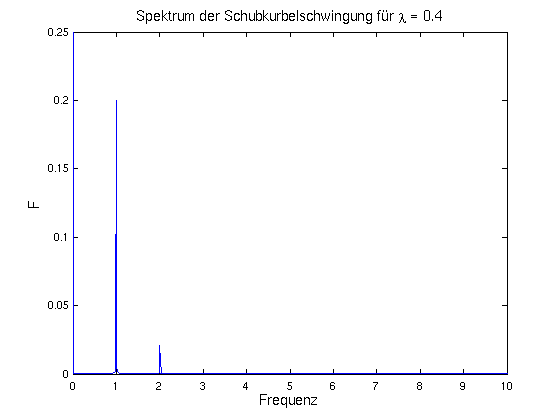
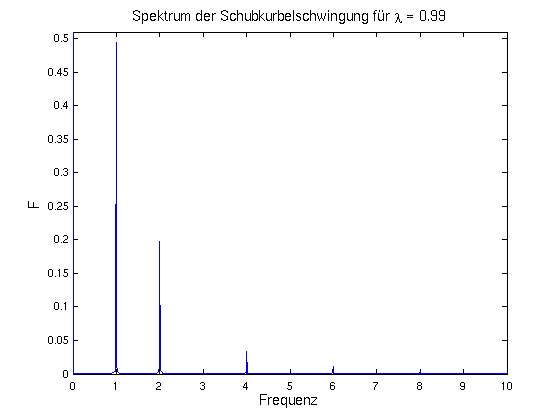
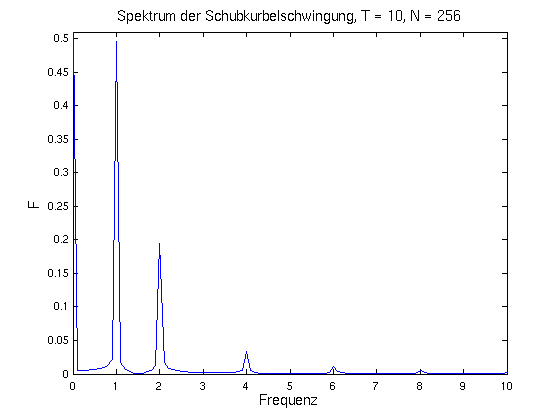
   • Um den interessanten Teil des Plots hervorzuheben, wird nur bis zur Frequenz f = 10 geplottet und die Skalierung von F so gewählt, dass der höchste Peak nach dem (alles überragenden) Mittelwert F(0) gut zu sehen ist. Man erhält
     • 
     • 
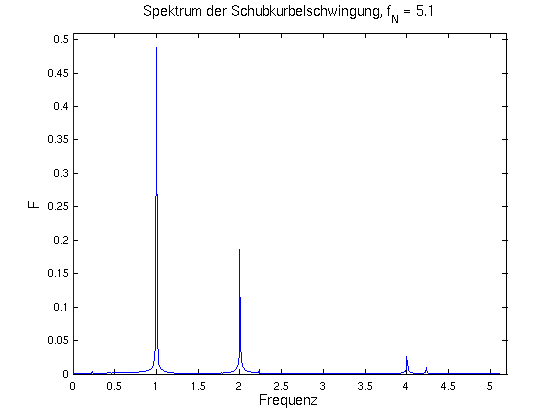
   • Verkleinert man N auf 1024, ist die Nyquist-Frequenz nur noch f_N = 5.115, die Oberwelle bei f = 6 ist jetzt als Peak bei 2 f_N - f = 4.230 zu sehen (Aliasing).
     • 
   • Verkleinert man T, verringert man damit die Frequenzauflösung, so dass sich die Peaks verbreitern. Ein großes N nützt hier nichts, sondern bewirkt aufgrund des großen f_N-Werts nur, dass auch (hier nicht vorkommende) sehr hohe Frequenzanteile noch aufgelöst werden.
     • 
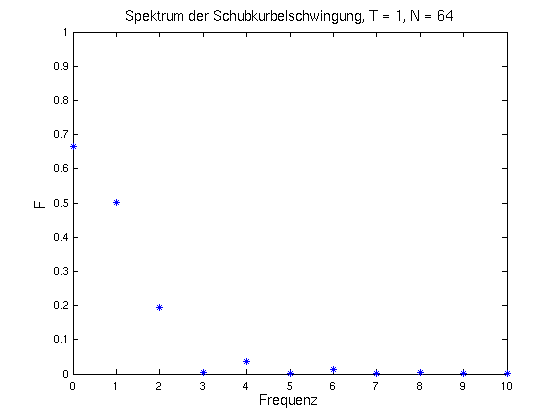
   • Der kleinstmögliche Wert für T ist natürlich T = 1, eine Schwingung.
     • 

• Reproduktion aller Ergebnisse mit dem Matlab-Skript ex14.m