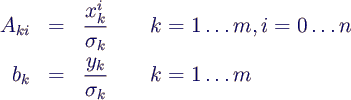Lösung von Aufgabe 12

• Alle numerischen Berechnungen können mit dem Matlab-Skript ex12.m ausgeführt werden.

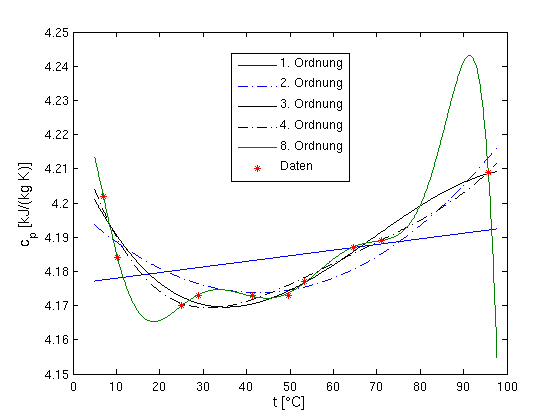
• Ausgleichskurven:
  • Ergebnis
    • 
  • Bewertung der Kurven
    • Die 8. Ordnung schwingt zu stark.
    • 1. und 2. Ordnung geben die generelle Tendenz nicht wieder
    • Tendenz der 3. Ordnung bei t > 70 °C sieht falsch aus
    • 4. Ordnung passt gut und schwingt nicht - optimal.
• Ausgleichspolynom für gewichtete Daten:
  • Da Matlabs polyfit-Funktion nicht mit gewichteten Daten umgehen kann, muss das Ausgleichsverfahren durchgeführt werden.
  • Matrix und rechte Seite des linearen Gleichungssystems erhält man aus
    • 
  • Hat man in Matlab die Werte in Spaltenvektoren t, cp und sigma gespeichert, kann man die Systemgrößen berechnen durch
    • sigma4Mat = sigma*ones(1, 5);
      A4 = [ones(length(t),1), t, t.^2, t.^3, t.^4]./sigma4Mat;
      b = cp./sigma;
  • Die Lösung des Ausgleichssystems erhält man mit
    • a4 = A4 \ b;
  • Für ein Matlab-Polynom muss man die Reihenfolge umdrehen (erster Koeffizient in Matlab = höchste Potenz)
    • poly4b = a4(5:-1:1);
  • Mit polyval erhält man somit die Werte für den Plot
    • 
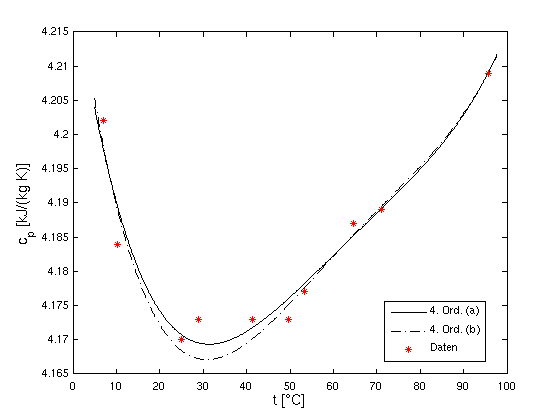
  • Vergleich a/b
    • Die Werte bei 30 °C und 40 °C haben einen deutlich größeren Messfehler, sie werden als "Ausreißer" weniger stark berücksichtigt. Die Ausgleichskurve verläuft daher tiefer, dichter an den anderen Punkten.