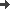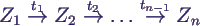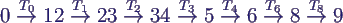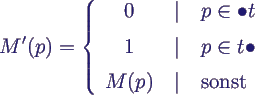Definition von Petri-Netzen
- Graphische Modellierung mit Petri-Netzen:
- eingeführt von Carl Petri 1962 (mathematisch)
- erweitert Zustandsautomaten um Prozesse = zeitliche
Abläufe
- ermöglicht u.a. Beschreibung paralleler Prozesse
- einfaches Grundmodell und viele Erweiterungen
- umfangreiche mathematische Analysen, z. B.
- Erreichbarkeit von Zuständen
- Beschränktheit von Plätzen
- Verklemmungsfreiheit
- Anwendungen u.a.
- parallele Prozesse in der Informatik
- Fertigungstechnik
- Logistik
- Geschäftsprozesse
- theoretische Biologie
- Grundaufbau eines Petri-Netzes:
- Graph mit
- zwei verschiedenen Arten von Knoten (Stellen
und Transitionen)
- gerichteten Kanten von Stellen zu Transitionen
und umgekehrt
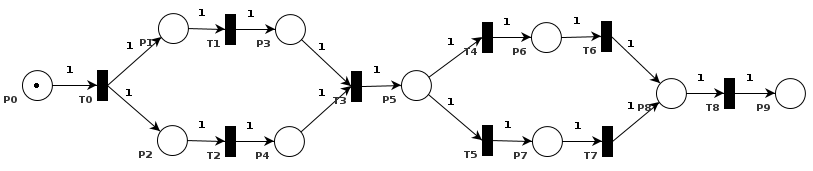
- Stellen (Places)
- rund dargestellt
- können eine oder mehrere Marken (Token)
enthalten
- beschreiben Teil-Zustände bzw.
Vor-/Nach-Bedingungen von Prozessen
- Transitionen
- schwarze Rechtecke (quadratisch bis sehr schlank)
- beschreiben Prozesse
- Prästellen einer
Transition t = Stellen mit Kanten zu t
- Poststellen einer
Transition t = Stellen mit Kanten von t
- Verhalten eines einfachen Petri-Netzes:
- Grundtyp: Stellen enthalten keine oder eine Marke
- Transition t heißt aktiviert
(enabled) ↔
- alle Prästellen von t enthalten eine Marke
- UND alle Poststellen von t sind leer
- aktivierte Transition t kann schalten →
- Marken aller Prästellen von t werden
vernichtet
- alle Poststellen von t erhalten eine Marke
- anschaulich: Marken wandern (incl.
Vernichtung/Erzeugung) durch Transitionen
- Wann schalten aktive Transitionen:
- sobald (externe) Bedingung erfüllt ist (cold
transition)
- automatisch (hot transition)
- bei mehreren aktiven Transitionen
- eine wird (zufällig oder gezielt)
ausgewählt
- mehrere können gleichzeitig schalten, falls
möglich
- im Beispiel: T4/T5 können nicht
gleichzeitig schalten
- Zeit zum Schalten
- instantan (beim Grundtyp)
- vorgegebene Schaltzeit einer Transition
- zufällige Schaltzeit einer Transition
- Beispiel "Bearbeitung einer Beschwerde":
- Petri-Netz von oben, Transitionen entsprechen
konkreten Prozessen
- Beschwerde kommt an (Token in P0)
- Beschwerde wird erfasst (T0 schaltet)
- Kunde wird angeschrieben und Abteilung angefragt (T1
und T2 schalten)
- beide Antworten werden zusammengeführt (T3
schaltet)
- Beschwerde wird akzeptiert (T4 schaltet)
- von den zwei aktivierten Transaktionen T4, T5
wurde T4 ausgewählt
- Kunde wird bezahlt (T6 schaltet)
- Vorgang wird abgelegt (T8 schaltet)
- Notation von Simulationsläufen:
- Zustand Z des Petrinetzes = Belegung der
Stellen
- bei einfachen Netzen reicht Liste der Stellen mit
Marken
- Darstellung einer Transition
- damit sequenzieller Ablaufplan
- bei unabhängigen Prozessen (im Beispiel T1/T2)
Reihenfolge wählen
- Beispiellauf damit etwa
- Unabhängigkeit von T1/T2 hier nicht darstellbar
- genauere Notation: verteilter Ablaufplan (distributed
run) [L6]
- Mathematisches Modell eines einfachen Petri-Netzes:
- gegeben durch 4 Größen (P, T, F, M0)
- P = Menge der Stellen
- T = Menge der Transitionen (mit P ∩ T =
∅)
- F ⊆ (P X T) ∪ (T X P) = Menge der Kanten
- M0: P → {0,1} = Anfangsbelegung
der Stellen (Markierung)
- für Transition t ist
- •t = {p | (p, t) ∈ F} (Prästellen
von t)
- t• = {p | (t , p) ∈ F } (Poststellen
von t)
- Markierung M: P → {0,1} = aktuelle Belegung der
Stellen
- Transition t ist aktiviert, wenn
- M(p) = 1 für alle p ∈ •t
- M(p) = 0 für alle p ∈ t•
- Schaltvorgang einer aktivierten Transition t
ändert Markierung M zu M' gemäß
- Anmerkung
- Was ist, wenn p zu •t und zu t•
gehört?
- Dann kann t nicht aktiviert sein!
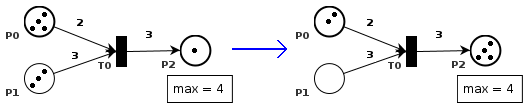
- Verallgemeinerungen:
- mehr als ein Token pro Platz möglich
- mehr als ein Token fließt ab bei Transition
- Transition t aktiviert ↔
- alle Prästellen von t enthalten
genügend Marken (gemäß Kanten zu t)
- UND alle Poststellen von t haben noch Platz
für Marken (gemäß Kanten von t)
- Transitionen brauchen Zeit zum Schalten
- pro Transition festgelegt
- alternativ stochastisch
- Marken haben Zusatzeigenschaften ("Farben")