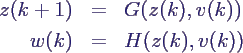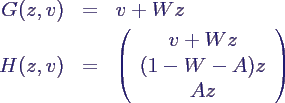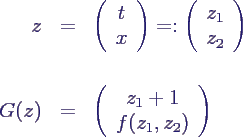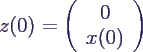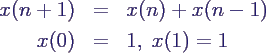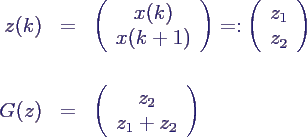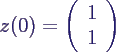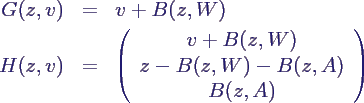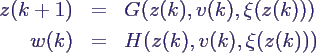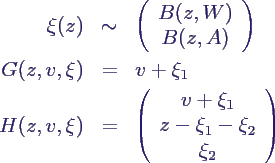Mathematische Beschreibung

• Zustandsraum-Darstellung:
  • verbreitete Beschreibungsweise diskreter Systeme und ihrer Komponenten
  • Grundidee
    • System bekommt Eingangswerte v(k)
    • ändert daraufhin seinen inneren Zustand z(k)
    • und produziert Ausgangswerte w(k)
  • v, z, w sind i. A. Vektoren (mehrerere Komponenten)
  • konkret
    • 
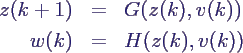
    • zusammen mit Startwert
    • z(0) = z₀
  • in Simulink leicht zu implementieren
    • 
  • Beschreibung komplexer Systeme
    
    • Zustandsraum-Darstellung für alle Komponenten
    • Gesamtsystem definiert über Verbindungen zwischen den Komponenten sowie externen Ein- und Ausgängen ("Simulink"-artig)
    • hierarchisch: auch Komponenten können durch Aufbau aus Subkomponenten beschrieben werden
    • alternativ:  Zustandsraumdarstellung für Komplettsystem, oft umständlich
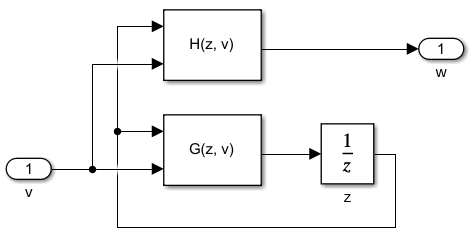
• Beispiel KlasseB:
  • Variablen
    • z = Ausgang des Unit Delay-Blocks
    • v = Eingangswert I
    • w = Vektor der Ausgangswerte [K, V, A]
  • Funktionen
    • 
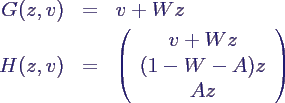
    • mit Parametern W, A
• Zustandsraum-Darstellung bei expliziter Zeitabhängigkeit:
  • Problem: z oder w hängen direkt von der Zeit n ab
  • Idee: Zustand enthält die Zeit
  • Beispiel Entwicklungsgleichung
    • x(n+1) = f(n, x(n))
    • keine Eingangs- und Ausgangswerte
    • z und G definiert durch
    • 
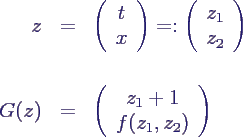
    • mit Anfangswert
    • 
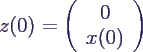
• Zustandsraum-Darstellung bei Abhängigkeit von früheren Zustandswerten:
  • Problem: neuer Zustandswert hängt von früheren Zustandswerten ab (nicht nur dem letzten)
  • Idee: Zustand enthält ältere Werte explizit
  • Beispiel Fibonacci-Folge
    • 
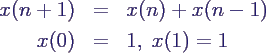
    • keine Eingangs- und Ausgangswerte
    • z und G definiert durch
    • 
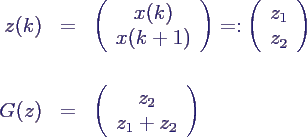
    • mit Anfangswert
    • 
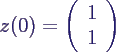
• Stochastische Zustandsraum-Darstellung [2]:
  • KlasseC enthält Zufallsgrößen, deren Verteilung B(z, W) von z abhängt
  • Variablen wie bei KlasseB
    
    • z = Ausgang des Unit Delay-Blocks
    • v = Eingangswert I
    • w = Vektor der Ausgangswerte [K, V, A]
  • Funktionen mit Hilfe von B(n,p)
    
    • 
  • Problem
    • B(z, W) kommt dreimal vor, ist aber immer dieselbe Zahl (analog B(z, A))
    • bei Implementation mit 3 Blöcken ergeben sich verschiedene Werte, Block darf also nur einmal im Modell vorkommen
    • besser: Symbol für einen konkreten Zufallswert kommt auch in der Beschreibung nur einmal vor
  • Erweiterung: stochastische Zustandsraum-Darstellung
    • neu: Zufallsvektor ξ(z), dessen Verteilung vom Wert des Zustandsvektors z abhängt
    • Gleichungen entsprechend erweitert
    • 
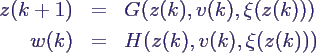
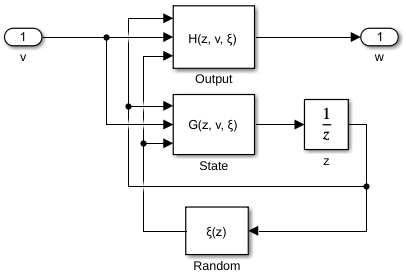
  • Implementation in Simulink
    • 
  • konkret für KlasseC
    
    • 
• Aufgaben:
  • Aufgabe 1
  • Aufgabe 2
  • Aufgabe 3