Simulation mit Zufallsgrößen

• Einbau stochastischer Größen:
  • zufällige Anzahl von Anmeldungen
    • "normalverteilt", aber ganzzahlig
    • Block Anmeldungen ersetzt Konstante
    • 
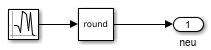
  • zufällige Anzahl von Wiederholern und Abbrechern
    • binomialverteilt B(n, p), n = Klassengröße, p = mittlere Quote
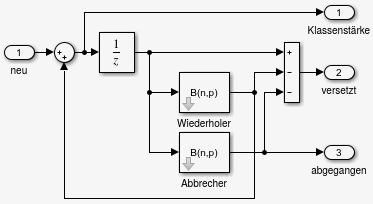
  • Block KlasseC hat dann ganzzahlige Klassengrößen
    • 
  • Ergebnis von schule3 sieht sinnvoll aus
    • 
• Block für B(n,p)-verteilte Zufallszahlen:
  • Anzahl n der Wiederholungen als Eingang
  • Erfolgswahrscheinlichkeit p als Parameter
  • Berechnung einfach mit Matlab-Funktion binomial.m
  • Parameter seed für Reproduzierbarkeit
    • seed ≥ 1  initialisiert Zufallszahlengenerator Rng
    • seed = -1 erzeugt neue Werte bei jedem Lauf (initialisiert mit Uhrzeit)
  • Problem
    • mehrere Blöcke setzen die seed für den gleichen Rng
    • der letzte (in irgendeiner Reihenfolge) setzt sich durch
  • Lösung
    • Blöcke haben normalerweise seed = 0, bewirkt nichts
    • nur ein Block bekommt anderen seed
    • vgl. Start-Callback startBinomial.m des Binomial-Blocks
  • genaues Verhalten von Binomial
    • Zufallszahl B(I,p) mit festem p und I vom Eingang
    • Wert I am Eingang wirkt sich sofort aus, d. h.
    • Binomial(k) = B(I(k), p)
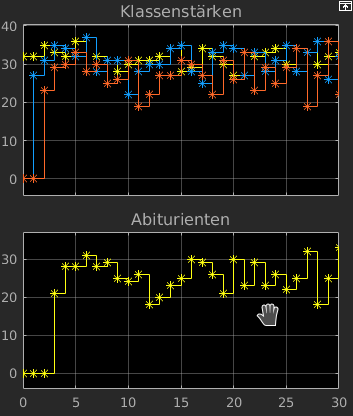
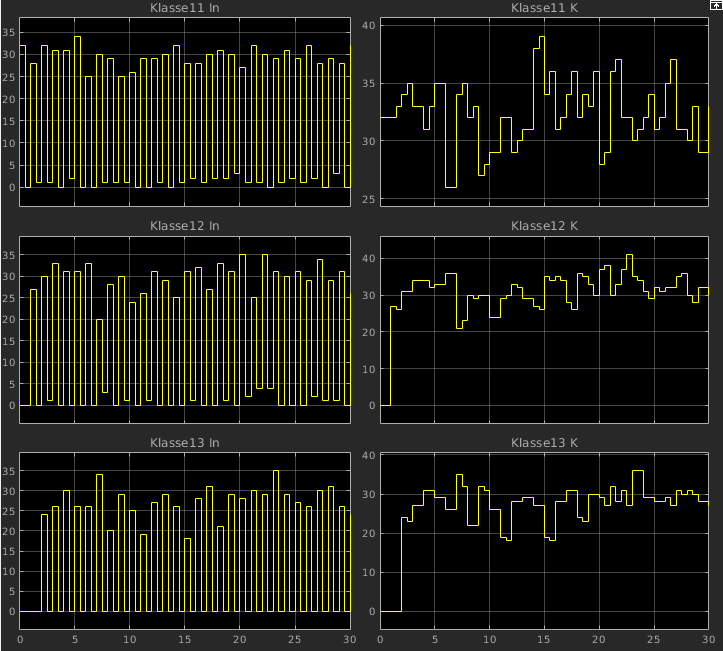
• Analyse des Ergebnisses:
  • Beobachtung
    • Einlaufphase, danach gleichmäßiges Verhalten
  • Wie beschreibt man die Klassengrößen?
    • stochastische Größen
    • ermitteln: Mittelwert und Standardabweichung
  • praktische Durchführung
    • Festlegung der Einlaufphase
    • ein langer Lauf oder viele kürzere Läufe?
  • vgl. Aufgabe 1
• Erweitertes Modell schule4:
  • zusätzlich: Rückstufung zum Halbjahr
  • Anzahl der Zurückgestuften: B(K, Z)
    • Z = mittlere Quote (Parameter)
    • K = Klassenstärke zu Beginn des Jahres
  • zum Halbjahr gehen einige (in die untere Klasse) und kommen einige (von der oberen Klasse)
    • KlasseD hat einen weiteren Ausgang Z, aber keinen weiteren Eingang
    • Eingang I enthält zu Beginn des Schuljahres und des Halbjahres jeweils verschiedene Werte
  • Abbrecher- und Wiederholerzahlen beziehen sich auf die Klassenstärke zu Beginn des 2. Halbjahres
    • diskutierbar, letzlich eine Frage der Definition der Quoten W und A
    • für Abbrecher komplexeres Modell denkbar, das Abbrecher für beide Halbjahre getrennt bestimmt
  • Signale mit verschiedenen Samplezeiten → Verhalten wird komplizierter!
    • Angabe der Samplezeiten als t_S = [Δt, t₀] → t_n = t₀ + n Δt
    • Klassenstärke jedes halbe Jahr, t_S = [0.5, 0]
    • Wiederholer und Abbrecher jedes volle Jahr, t_S = [1, 0]
    • Zurückgestufte jährlich zum Halbjahr, t_S = [1, 0.5]
  • Gesamtmodell
    • 
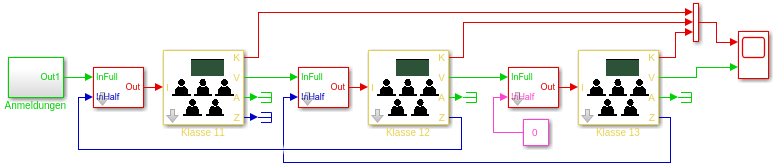
    • farbige Darstellung der Samplezeiten mit Display/Sample Time/Colors
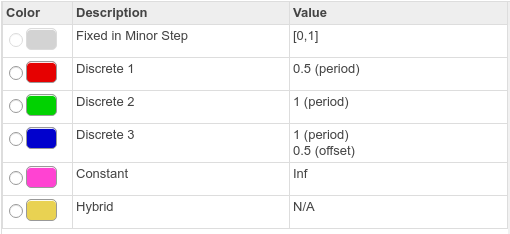
    • Legende für die Farben
    • 
  • Komponente TimeSwitch
    • führt Signale mit t_S = [1, 0] und t_S = [1, 0.5] zusammen zu einem Signal mit t_S = [0.5, 0]
    • 
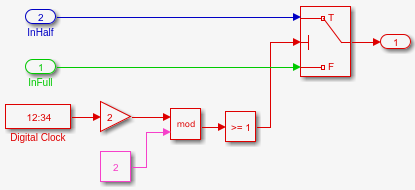
    • DigitalClock mit Sample Time = 0.5
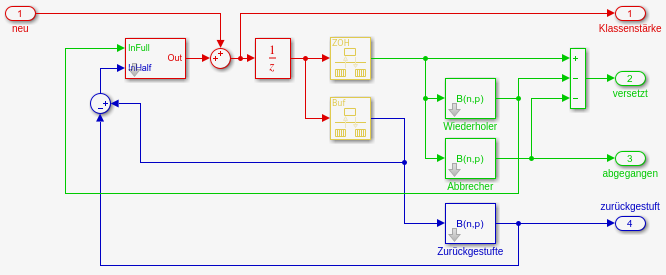
• Implementierung von KlasseD:
  • Aufbau
    • 
  • Block Unit Delay hat Sample Time = [0.5, 0]
  • Block RateTransition
    • legt Sample Time des Ausgangs fest
    • oben [1,0] → merkt sich den Wert bei t = n für 1 s
    • unten [1,0.5] → merkt sich den Wert bei t = n+0.5 für 1 s
    • unten Parameter Ensure deterministic data transfer ausgeschaltet!
  • Eingang des Unit Delay
    • volles Jahr: neue vom Eingang (= Versetzte) + Wiederholer
    • Halbjahr: Zurückgestufte vom Eingang + (Klassenstärke - Zurückgestufte)
• Testen von KlasseD:
  • komplexes Modell, einzeln genau testen!
  • einfaches Testmodell testKlasseD
    • 
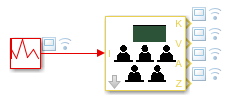
    • Eingangswerte für I (mit Taktrate = 0.5, Start bei 0)
    •  [100 10 200 20 100 10]
  • Parameter von KlasseD
    • W = 0.2, A = 0.1, Z = 0.1
    • ermöglicht überschlägige Plausibilitätsprüfung der Zufallszahlen
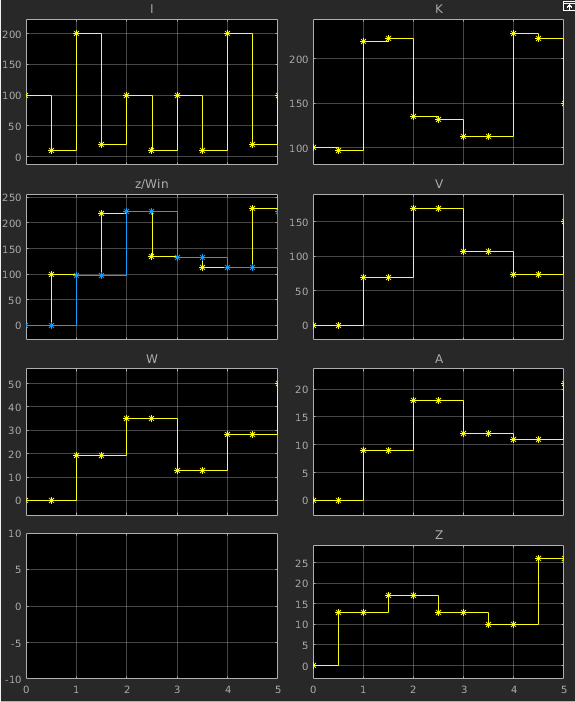
  • Darstellung relevanter Signale
    • 
  • zusätzlich zu den Anschlüssen sind dargestellt
    
    • W: Zahl der Wiederholer
    • z/Win: Ausgang des Unit Delay/Eingang des Wiederholer-Blocks
  • erscheint plausibel
  • genauer: manuelle Prüfung der Werte

    • t	I	K	Z	W	A	V
      0.0	100	100	-	0	0	0
      0.5	10	97	13	-	-	-
      1.0	200	219	-	19	9	69
      1.5	20	222	17	-	-	-
      2.0	100	135	-	35	18	169
      2.5	10	132	13	-	-	-
      3.0	100	113	-	13*	12	107

  • alles ok, lediglich der *-Wert ist etwas klein
    • n = 132, p = 0.2, damit
    • 
    • Abweichung knapp 3σ
    • Überprüfung: Eingang Win(t = 3) = 132, ok
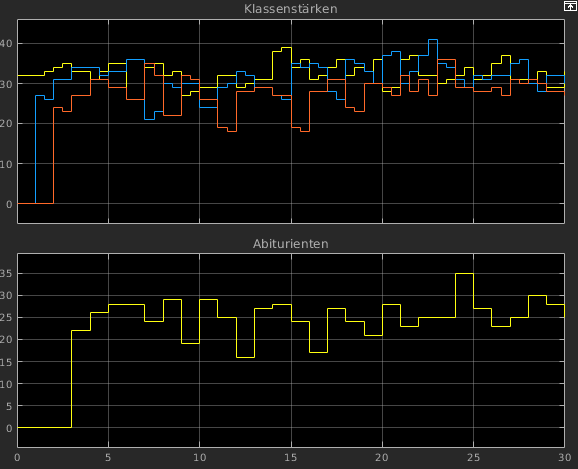
• Ergebnis von schule4:
  • Gesamtergebnis
    • 
  • detailliert zur Prüfung
    • 
  • sieht sinnvoll aus
  • Modell grob verifiziert
    • Validierung: Vergleich der benutzten Zufallsverteilungen mit realen Werten
  • schließlich "Arbeitsläufe" und statistische Analyse der Ergebnisse