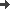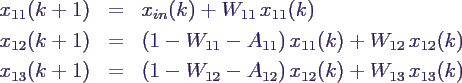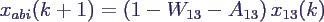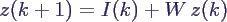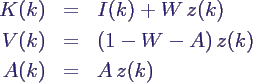Modellierung einer Schule

• Grundprinzip:
  • Zustandsgrößen x(t) ändern sich in festen Zeitabständen t_i (getaktet)
    • t_n = n Δt, n = 0, 1, 2, ...
    • Größe des Zeitschritts (Sample time) Δt
  • Verhalten der Zustandsgrößen x_n ≡ x(n) nicht durch DGLs beschrieben, sondern z. B. durch Entwicklungsgleichungen
    • x(n+1) = f(n, x(n)), n = 0, 1, 2, ...
    • Startwert x(0) gegeben
  • häufig hängt f nicht vom aktuellen Zeitschritt n ab (zeitunabhängig)
• Beispiel "Schülerzahlen einer Oberstufe":
  • Zahl der Schüler x₁₁, x₁₂, x₁₃ in Klassen 11, 12, 13
  • ändern sich in jedem Jahr durch
    • Zugang x_in in der 11. Klasse
    • Zahl der Wiederholer, Anteil W₁₁, W₁₂ etc.
    • Zahl der Abbrecher, Anteil A₁₁ etc.
    • Zahl der versetzten Schüler vom letzten Jahr
  • insgesamt beschrieben durch die Gleichungen
    • 
  • Zahl der Abiturienten gegeben durch
    • 
  • genaue Bedeutung
    • x₁₁(k) = Klassenstärke zu Beginn des Schuljahres k
  • Fragestellungen
    • Wie groß sind die (voraussichtlichen) Klassengrößen?
    • Wieviele fertige Abiturienten gibt es jedes Jahr?
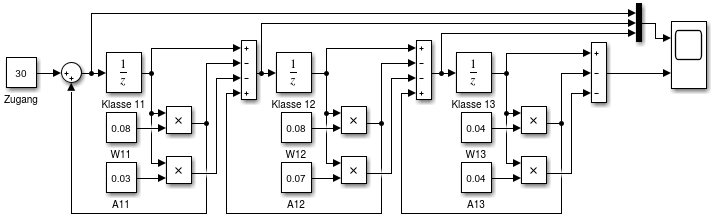
• Modellierung in Simulink:
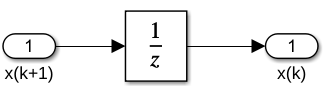
  • zentraler Block: Discrete/Unit Delay
    • verzögert Wert um einen (diskreten) Simulationsschritt
    • übernimmt Rolle von Integralblock ("1/s") bei kontinuierlichen Systemen
    • 
  • Parameter von Unit Delay
    • Initial condition = Startwert x(0)
    • Sample Time = Schrittweite
    • besser: Sample Time = -1 und Wert im Solver vorgeben
  • Simulationsparameter
    • Solver type: Fixed-step
    • Solver: discrete (no continuous states)
    • Fixed-step size: 1 ("ein Jahr")
  • Komplettmodell schule1
    • 
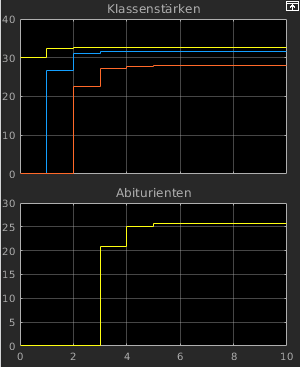
  • Anzeige der Klassenstärken x_N(k) und der Zahl der Abiturienten x_abi(k)
    • 
• Darstellung der Ergebnisse:
  • Style = Auto (hier = Stairs)
    • liefert durchgängige Kurven, x(k) hat konstanten Wert für k ∊ (n, n+1)
    • welcher Wert gilt an der Sprungstelle?
  • Style = Stem
    • 
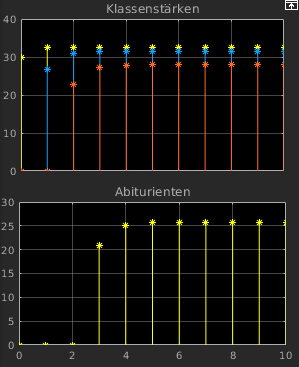
    • präziser, x(k) nur definiert für k ganzzahlig
    • oft unübersichtlich
  • Style = Stairs + Marker
    
    • 
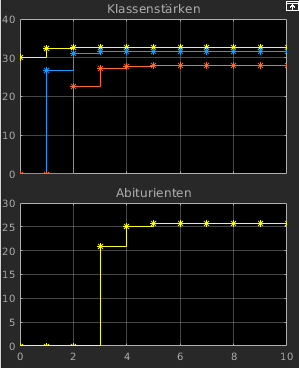
    • häufig guter Kompromiss
  • sinnvolle Darstellung schützt vor Fehlinterpretation der Ergebnisse!
• Übersichtlichkeit durch Hierarchien von Komponenten:
  • Problem
    • schule1 ist komplex und unübersichtlich
    • Blockstruktur wiederholt sich für jede Schulklasse
  • Lösung: eigener Block KlasseB zur Beschreibung einer Klasse
  • Eingang
    • I = Zahl neuer Schüler (aus unterer Klasse)
  • Ausgänge
    • K = Klassenstärke (zu Beginn des Schuljahres)
    • V = Zahl der versetzten Schüler (der vorigen Klasse!)
    • A = Zahl der abbrechenden Schüler (der vorigen Klasse!)
  • fertiges Submodell
    • 
  • Maske erstellen mit
    • Parameter für Wiederholer- und Abbrecherrate sowie Anfangsstärke
    • Icon und Beschriftung der Anschlüsse
    • Hilfstext
  • eigene Block-Library discSimLib für neuen Block (und weitere)
    • Gesamtmodell enthält nur einen Verweis
    • Änderung des Bibliotheksblocks aktualisiert alle Instanzen
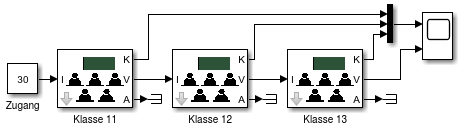
  • Gesamtmodell schule2
    • 
  • Zahl der Abgänger wird nicht verwendet
    • erzeugt Warnungen im Matlab-Fenster
    • unterbinden mit Terminator-Block
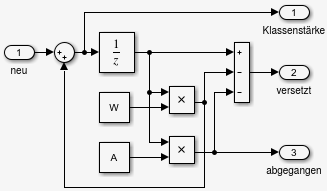
• Mathematische Beschreibung des Blocks KlasseB:
  • definiere Zustandsgröße z(k) als Ausgang des Unit Delay-Blocks zur Zeit k
  • Parameter W, A durch Maske gegeben
  • Eingangswert I(k) zur Zeit k
  • Berechnung des nächsten Zustandswerts
    • 
  • Berechnung der Ausgangswerte
    •