Systeme mit State-Events
- Eigenschaften hybrider Systeme:
- haben kontinuierliche Zustandsgrößen sowie diskrete
Events (und evtl. diskrete Zustandsgrößen)
- große Vielfalt
- kontinuierliche Systeme mit Unstetigkeiten (Bsp.
Hüpfender Ball)
- diskrete Umschaltung zwischen kontinuierlichen
Systemen (Bsp. Fadenpendel mit Freiflug-Phase)
- diskrete Systeme mit kontinuierlichen Subsystemen
(Bsp. Muffelofen)
- Simulation schwierig (vgl. Argesim-Benchmark C21 [20])
- meist Kombination verschiedener Methoden
- Ansätze häufig ausgehend von DGLs oder ausgehend
von Ereignissteuerung
- Mathematische Beschreibungsmethoden:
- sehr verschiedene Ansätze je nach Ausgangspunkt
- bisher kein allgemein verbreitetes universelles
Hybrid-Modell
- Hybrid DAEs [21]
- Ausgangspunkt kontinuierlich (DAEs)
- Einführen verschiedener Klassen von Ereignissen [20]
- Details je nach möglichen Event-Typen
unterschiedlich
- DEV&DESS [L8]
- Kombination von DEVS und DESS ("Differential
Equation System Specification")
- DESS = einfache Zustandsraum-Beschreibung von
DGLs incl. Eingangs- und Ausgangsgrößen
- Kopplung zwischen DEVS- und DESS-Größen
- DEVS mit QSS ("Quantized State Systems") [L8]
- Idee: DGLs müssen zur Simulation sowieso
diskretisiert werden
- statt der Zeit werden hier die Zustände der DGLs
diskretisiert
- damit wird DGL-Anteil durch DEVS beschrieben
- entsprechende QSS-DGL-Solver wurden entwickelt
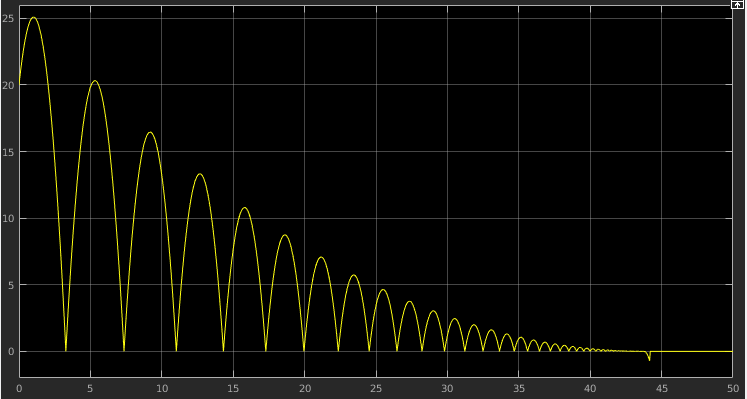
- Beispiel "hüpfender Ball":
- System
- Ball fällt senkrecht herunter
- prallt am Boden ab, verliert dabei Energie
- Modell
- DGL zur Beschreibung des Falls
- Abprall als instantan vereinfacht
- Höhe wird 0 → v ändert sein Vorzeichen, sein
Betrag nimmt um festen Faktor ab
- grundsätzlich kontinuierliche Zustandsgrößen, aber
zusätzliche Events
- Zeitpunkt der Events nicht vorher bekannt
- Zustände ändern sich bei Event (ggf. unstetig)
- State-Change Event SE-X in Nomenklatur von [20]
- DGL-Solver mit Events:
- Solver bekommt Funktion h(t,y) zur Event-Definition
(zusätzlich zu f(t,y))
- Event = "h wird 0"
- Solver führt Schritt durch und prüft, ob Vorzeichen
von h wechselt
- nein → nächster Schritt wird berechnet
- falls ja
- genauer Zeitpunkt tE des Events wird
bestimmt (z. B. durch Newton-Verfahren)
- Solver löst DGL bis tE und stoppt
- Zustandsgrößen können geändert werden
- Solver wird von tE an neu gestartet
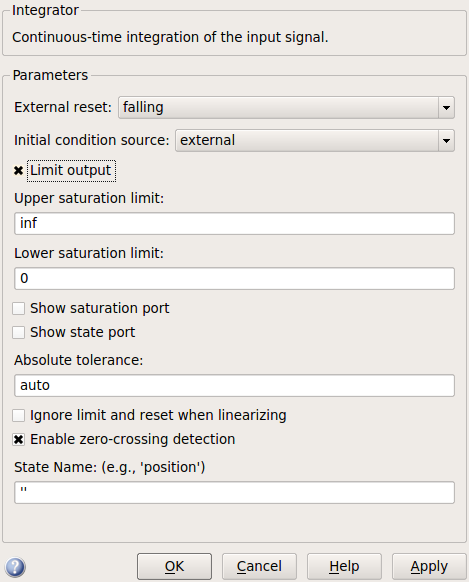
- Implementierung in Simulink mit Integrator-Block:
- Parameter
- Beschränkung des Ergebnis-Bereichs (saturation
limits)
- optionales Signal bei Überschreiten und Verlassen
der Grenzwerte (saturation port)
- Eingangssignal zum Zurücksetzen auf Anfangswerte (external reset)
- Eingangssignal zur externen Festlegung der
Anfangsbedingung (initial condition source
= external)
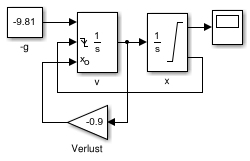
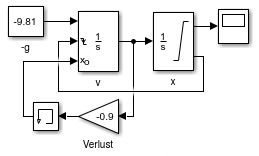
- Modell huepfballA:
- Aufbau
- Funktionsweise
- x-Integrator ist eingeschränkt auf [0, Inf]
- saturation port liefert
negatives Triggersignal bei Erreichen von x = 0
- v-Integrator wird dadurch auf Anfangswert
zurückgesetzt
- Anfangswert ist -0.9*aktueller Wert
- Ergebnis:
- hüpft nicht, sondern bleibt liegen
- Ursache: algebraischer Schleife bei v
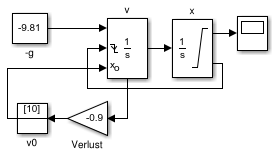
- Modell huepfballB:
- Abhilfe: state port = Integrator-Ausgang zur Zeit t,
vor dem Reset
- durchbricht algebraische Schleife
- Aufbau
- zusätzliches v0 durch Initial
Condition-Block
- Ergebnis: funktioniert
- interessanter Effekt
- zero-crossing detection
bei beiden Integratoren ausschalten
- Ursache: Solver bekommt keine Event-Funktion mehr
- Zenon-Effekt:
- Modell huepfballB bis t=50
laufen lassen → Fehlermeldung
- At time 43.997112102528291,
simulation hits (1000) consecutive zero crossings.
- Ursache: unendliche viele Hüpfer in endlicher Zeit (Zenon-Effekt)
- Abhilfe: Solver-Parameter
Zero-crossing options/Algorithm auf Adaptive
- Ergebnis von Modell huepfballC
- alternativ Memory-Block
statt state port → klappt ohne "Zacke" auch bei
Algorithm auf Non-adaptive (huepfballD)
- genauere Untersuchung nötig (vgl. [20])