Example 4: Distribution of compressed air
- Basic system:
- simple pneumatic system with pressure source, tee
branch, pipe and consumers
- Model in Modelica:
- uses PneuBib library
- PneuBib itself based on MSL Fluid library
- MSL Fluid library basically describes quasistatic
processes
- run in Dymola →
- Warning: Failed to solve nonlinear system using
Newton solver...
Error message from dymosim
At time T = 5.130275e-04 ... the corrector could not converge
because there were model evaluation failures and the stepsize
cannot be reduced further.
Integration will be terminated.
- Mathematical problem:
- model consists of 170 equations, many are coupled and
highly non-linear
- proper initial values are unknown and guessed by
solver
- → Newton solver does not converge
- well-known problem of MSL Fluid library
- Reality check:
- system starts with ambient pressure and zero mass
flow everywhere
- switching on pumps etc.
- → global pressure difference increases
- → mass flows increase slowly due to mass inertia
- → local pressure differences build up
- Extended Model:
- introduce inertial pressure difference Δr
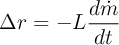
- inertance L is given by geometry of a component
- can be derived from Euler equation
- split pressure into quasi-static part
 and inertial part
and inertial part
- at junctions use
 instead of p
instead of p
- approximation of transient behaviour
- leads to decoupling of component equations
- consequences
- independent small non-linear parts instead of a
huge coupled system
- total coupling by relaxation using simple linear
ODE
- new parameter L (usually having default value)
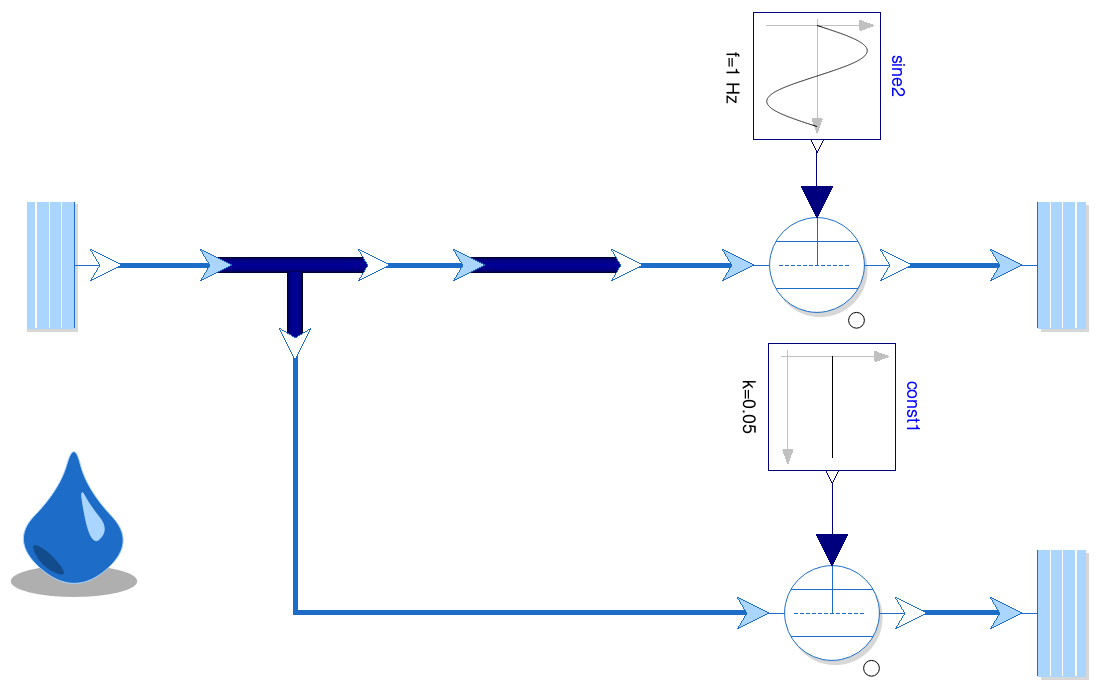
- free DLR ThermoFluidStream Library
- provides components for vessels, pipes and
machines based on these ideas
- use it to model pneumatic system → runs
- result
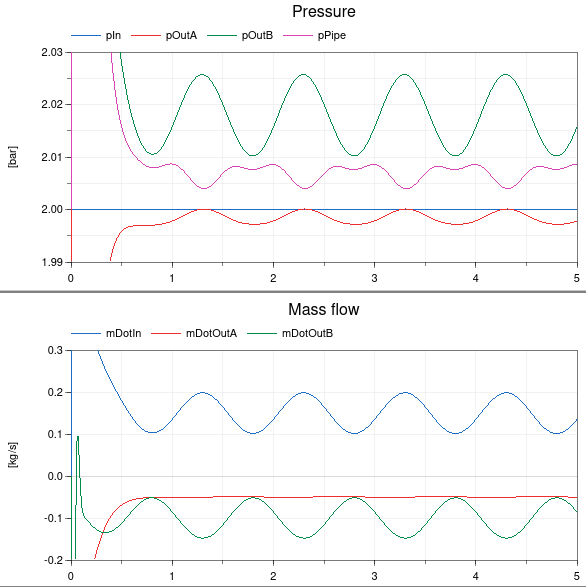
- approximate relaxation for t < 1
- quasistatic behaviour for t > 1
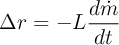
 and inertial part
and inertial part
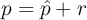
 instead of p
instead of p
